Compounding is one of the most important concepts in finance. It’s a repetitive process that can create exponential growth in savings and investments.
How does it work?
Simply put, compounding is the effect of earning interest on interest (or additional profits on previous investment profits).
Consider the following example:
- In year one, you invest £3,000 in a simple interest-bearing account that pays 5%,
- By the end of the year, you’ll have £3,150.
- You then reinvest this in year two at the same rate of interest but the 5% now gets paid on the larger number – i.e. you’re now earning interest on £3,150 rather than £3,000.
In the first few years, the effect of compounding is relatively small, however, in the long run, it can have a huge impact.
This is illustrated in the chart below, which shows the effect of compounding on that same £3,000 a year saving, earning 5% interest, over 40 years:
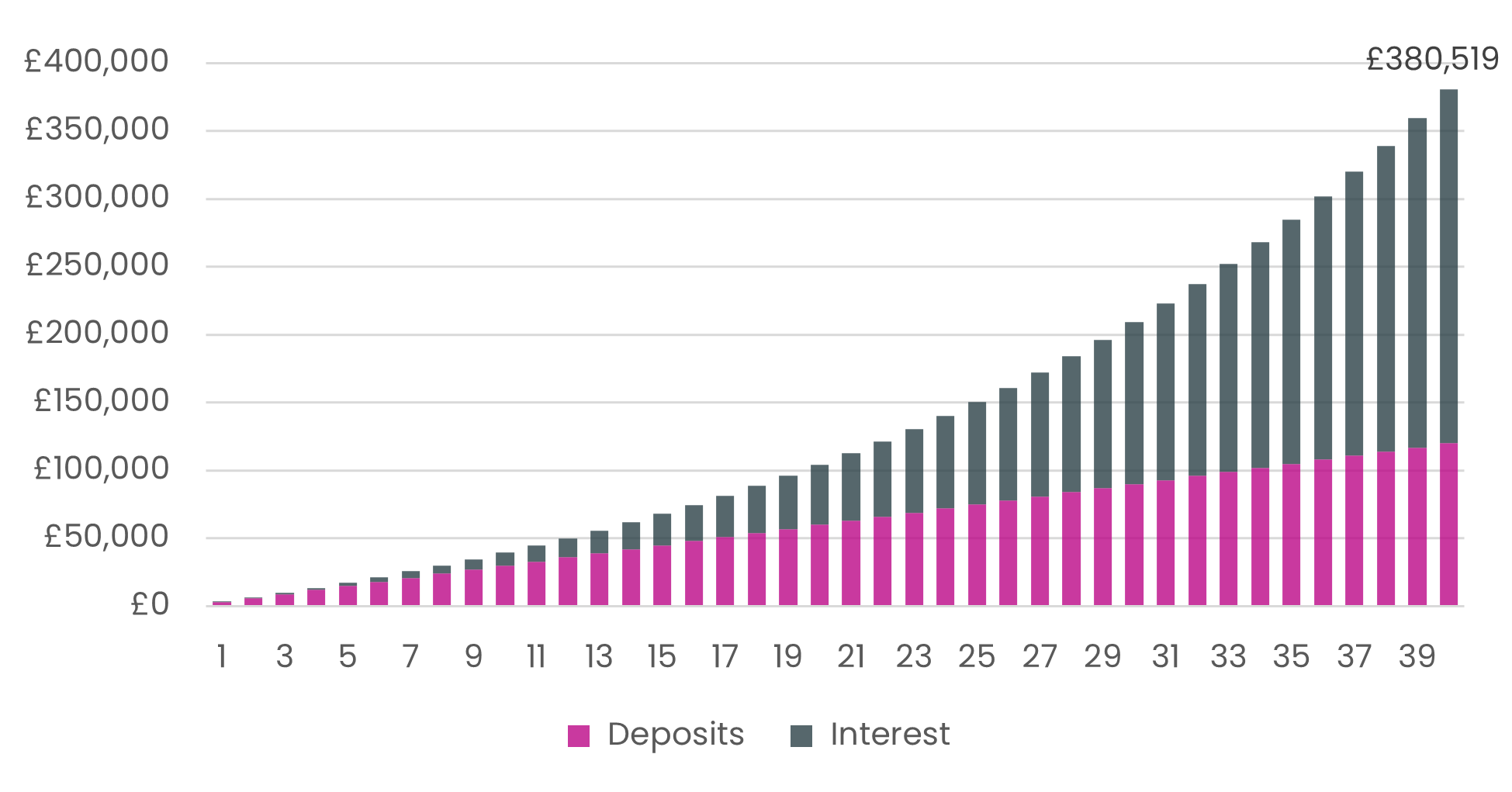
That is, after 40 years, you would have made total deposits worth £120,000 (£3k a year for 40 years), but would now have an investment worth £380,519. The rapid ascension in value over the final 10-15 years reflects the effect of compounding – the widening dark blue ‘interest’ bars in the chart above - as you earn additional interest on interest.
What a difference a decade makes…
The above is fairly straightforward and will be well-known to most readers.
But here are a couple of examples to show just how powerful compound interest can be, along with the costs of delaying saving to a later stage.
Example 1
- Claire is a disciplined saver. At age 25, she invests £10k and follows this up with £5k a year until age 65 (assumed retirement age).
- In contrast, Charlie defers commencing his ‘investment journey’ until he is earning more. At age 35 (i.e. a decade later than Claire), he invests £20k and then £10k a year until age 65.
In both cases, the money is invested in a well-diversified portfolio of global equities, earning an average return of 7% a year.
Who has more money at age 65?
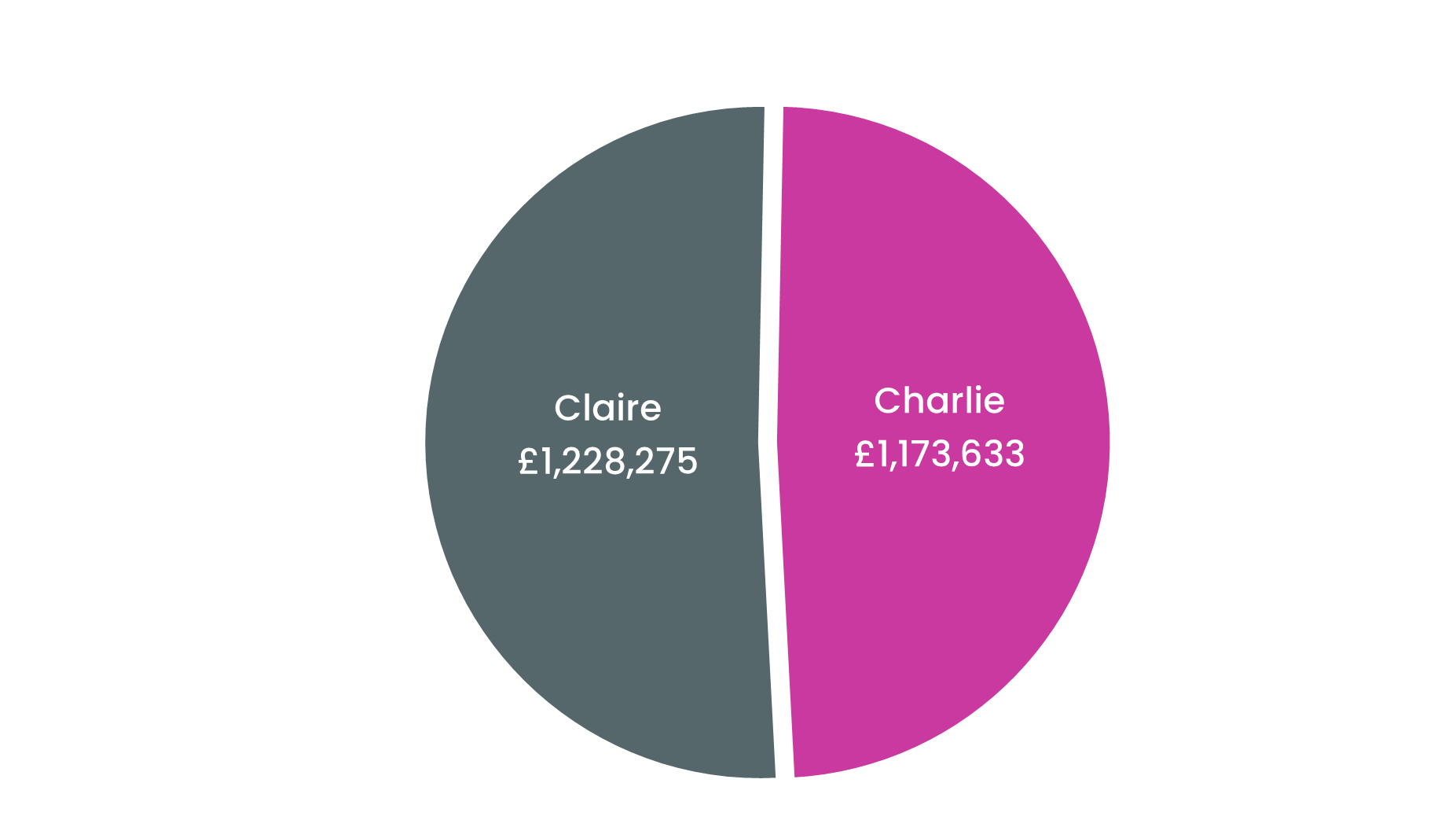
Charlie invested 52% more than Claire – a total of £320k vs £210k, and twice as much per annum for 30 years. However, Claire ends up with more money because she started ten years earlier.
Another way to look at compounding and time is to consider how much money you’d need to invest each year to reach say £1m at the point of retirement, but starting at different points in time.
Example 2
Consider the table below:
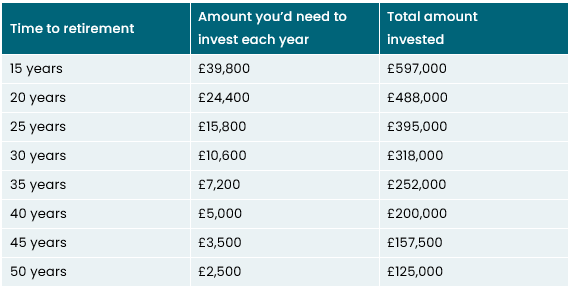
That is, to reach £1m in retirement savings, someone starting 15 years prior would need to invest almost £40k a year or £597k in total. Whereas someone starting 50 years prior, would ‘only’ need to invest £2,500 a year or £125k in total.
In fact, for every ten years of waiting, you’d need to invest around twice as much per year to reach the same eventual retirement goal - £1m in this case.
Disclaimer: The above assumes annual investment returns of 7% a year net of costs. The above are for illustrative purposes only and do not take into consideration any investment performance. Your capital is at risk. The value of your investment (and any income from them) can go down as well as up and you may not get back the full amount you invested. Past performance is not a reliable indicator of future performance.
The conclusion is simple – start early and let compounding do the work.
As the late, great, Charlie Munger once said “Understanding both the power of compound interest and the difficulty of getting it is the heart and soul of understanding a lot of things.”
Disclaimer: This blog is for general information only and does not constitute advice. The information is aimed at retail clients only. Since I don’t know your specific situation, none of this information should be construed as tax or financial advice. It is not an offer to purchase or sell any particular asset and it does not contain all the information which an investor may require to make an investment decision. Although endeavours have been made to provide accurate and timely information, there can be no guarantee that such information is accurate as of the date it is received or that it will continue to be accurate in the future. We cannot accept responsibility for any loss as a result of acts or omissions taken in respect of any articles


